Systems Diagrams

Understanding How Factors Affect One Another

© iStockphoto/mevans

System diagrams are powerful tools that help you to understand how complex systems work. Systems analyzed may be anything from businesses, through biological population models, to the impact of social policy, etc.

System diagrams are particularly helpful in showing you how a change in one factor may impact elsewhere. They are excellent tools for flushing out the long term impacts of a change. Importantly, a good system diagram will show how changing a factor may feed back to affect itself!

Drawing a system diagram is a good way of starting to build a computer model. The technique helps you to map out the structure of the system to be modeled. It shows the factors and relationships that are important, and helps you to start quantifying the linkages between factors.

How to Use the Tool

Relationships Between Factors

At the heart of the use of system diagrams is the idea of linking factors to show a relationship between them.

For example a company may link the factors of product quality and customer satisfaction. It believes that as the quality of its goods change, so will customers' happiness with them. We show this as an arrow linking the two factors:

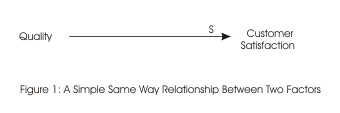
The S shows that the factors move in the Same way – as quality improves, so will the happiness of customers. The arrow shows the direction of the relationship: raising customer happiness does not necessarily raise the quality of the goods!

These relationships can also work the other way. The company may link price with the customers' perceptions of the 'good value' of its goods. This is shown below:

The O shows that the relationship works in the opposite way: in this case as you raise price, customers' perceptions of good value reduce.

Feedback Loops

Feedback is an important concept in the use of system diagrams – in very many cases changing one factor will impact on another factor, which will then affect the first.

Feedback will either reduce the impact of the change, or will amplify it.

Balancing Loops

Where feedback reduces the impact of a change, we call this a Balancing Loop. The example below shows an example of a balancing loop, where an under-resourced service company is trying to raise quality:

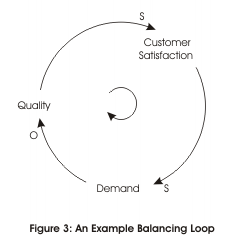
In this situation, improving the quality of service leads to improved customer satisfaction, which leads to an increase in demand for the company's service. In trying to meet this demand, the company has less time to devote to individual customers, which reduces its ability to improve quality further.

Note the small circular arrow in the middle of the loop. This shows which way round the loop is running. In complex diagrams with many loops, this arrow will be labeled and will identify loops.

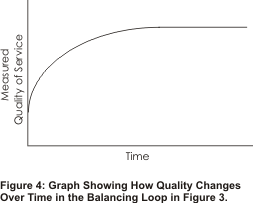
The graph below shows how quality of service might vary with time in the example above:

Reinforcing Loops

Where feedback increases the impact of a change, we call this a Reinforcing Loop. The example below shows an example of a theatre trying to improve its profitability by investing more in productions.

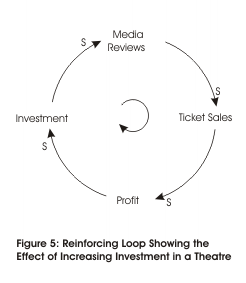
As more investment is put into a production, the theatre is able to put on more lavish plays with more famous actors. Better plays should bring better reviews, and therefore higher ticket sales. This should lead to higher profitability, and therefore more money available to invest in future productions.

A graph showing how ticket sales might vary against time is shown below:

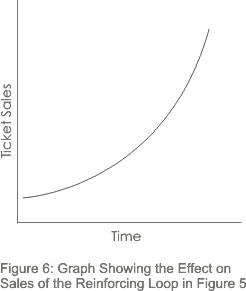
Note that this assumes that investment is increasing as time goes on. It also ignores some important facts: firstly that there are only a certain number of seats in the theatre, and secondly that external factors such as competition and market saturation will eventually limit growth. On a system diagram showing the way that the theatre operates, these factors would be shown as balancing loops impacting on this reinforcing loop.

External Factors

The system diagrams we have looked at so far completely ignore the impact of these external factors on them.

In our balancing loop example above we assumed that demand was raised only as customers became more satisfied. In reality demand is just as likely to be affected by the state of the economy. This is shown in the modified diagram below:

We show an external factor as a labeled relationship arrow pointing to the appropriate part of the system diagram.

Gaps

In our reinforcing loop example above we related sales of theatre seats to investment in productions. What we were not able to build into the model was the fact that there is a limited number of seats in the theatre.

Inevitably this will cap the growth of ticket sales as the theatre will seriously upset customers if it sells more tickets than it has seats available!

We build this into our model with the idea of a gap. There is a gap between the number of seats available (an external factor we have not yet built into our model), and the number of seats used (tickets sold).

As the theatre sells more tickets, the size of this gap reduces. At a particular point it cannot sell any more tickets. Increases in investment beyond this point may not yield any more profit.

We show this by modifying our diagram to both show both the external factor of the limit of the number of seats, and to show the gap:

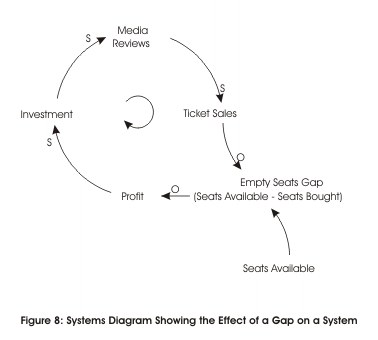
When all seats are sold, i.e. when seats available – seats bought = 0, then profit will not rise any higher unless other factors are brought into the system.

Note that it is very important to get the gap definition correct for your model.

Delay

The impact of delay is the final area we need to consider in our system diagrams.

Ideally when we make a change to a system it should adjust immediately to its new state. In reality there is almost always a delay before other factors adjust. This delay may occur in a mechanical system simply as a result of inertia and friction. In a human system it will occur as people take time to communicate, get used to new ideas, and implement change.

We can show this delay in a simple model using antelopes and cheetahs. As the number of antelopes rises, more food is available for the cheetahs. More cheetahs will therefore survive, and will be able to breed.

One part of the delay within this system is given by the length of time it takes for a cheetah to be born and grow to maturity. The other part occurs as starving cheetahs take time to die.

Feedback occurs as cheetahs kill antelopes. The higher the number of cheetahs, the greater will be their impact on the antelope population.

The system below shows this:

Note the double slash on the line showing the relationship between the antelope and cheetah populations. This shows that some form of delay is slowing the change of the related factor.

If there was no delay within the system, we might expect to see a graph showing the number of cheetahs over time like the one below:

Here adjustment would be immediate. Any change in the antelope population would be instantly matched by an increase in the cheetah population. These additional cheetahs would eat the additional antelopes, and then die immediately.

The delay in the system causes it to behave in a different way:

• Firstly the cheetah population will take time to increase
• Next, the large population of cheetahs will continue to breed as food starts to become scarce.
• This number of cheetahs will cause a big reduction in the number of antelopes.
• This will then lead to a crash in cheetah population as animals starve.
• The antelope population will then recover as there will be fewer cheetahs to restrict their numbers.

If nothing else has any impact on this system, then cheetah numbers may oscillate as shown below:

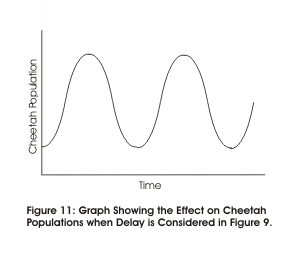
This occurs as the cheetah population continually over-adjusts, first in growth, and then in decline. In this system, the longer it takes for a cheetah to breed and starve – i.e. the greater the delay – the greater will be the variations in cheetah populations.

Improving the Systems Model

The models we have looked at so far have been simple – they have ignored many possible impacts on each system. For example, in our model of antelopes and cheetahs, we have ignored the impact of disease, drought, human activity, etc.

We improve the model by building in as many of these external factors as we can think of. We can then simplify it by eliminating those factors that have a negligible impact.

External factors might be:

• Natural – weather, natural resources, disease, environmental change, etc.
• Technological – new technologies, changes in technology, etc.
• Human – psychological, emotional, ambitions, expectations, etc.
• Political – ideology, corruption, effectiveness, interest, etc.
• Social – values, social inertia, traditions, philosophies, etc.
• Financial – state of the economy, capital available, etc.

Ultimately you may end up with a model made up of a number of reinforcing loops, balancing loops and external factors. The example below shows a more sophisticated diagram of the antelopes and cheetahs system:

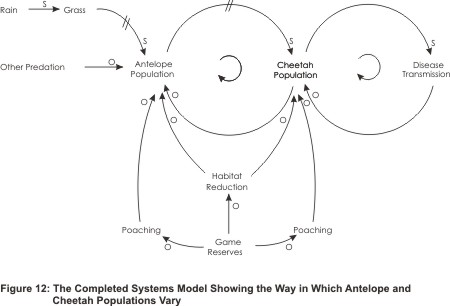
Note: This diagram is an example only and does not necessarily reflect how antelope and cheetah populations operate in real life.

Systems Diagrams as the Basis of Computer Models

Once you have established the relationships between factors on your diagram, you can look to see if you can put numbers to the relationships. In the example above you may find that if drought halves the amount of grass available to antelopes, that the antelope population reduces by one third.

You can build this relationship into a computer model. A useful way of starting this with simple and moderately complex models is to build the model on a spreadsheet.

You can use this model to make predictions by changing factors within it. This would allow you to assess the likely impact on your system of external changes, and investigate the effect of changes you might make within the system.

Key Points

Systems diagrams allow you to model the way in which complex systems work. They help you to think through the way in which the factors within a system interact and feed back upon themselves.

You should now be able to analyze:

• How factors are related, and how one factor will change when another changes.
• How factors may feed back in either balancing loops or reinforcing loops.
• How external factors impact on the system.
• How gaps operate.
• How delay affects the system.
• All the complexities of a system.