Using Reason to Predict Future Behavior

When is the right time to "pounce"?
© iStockphoto/EEI_Tony
What if you could make good predictions about how competitors will respond to your actions?
What if you could take this into account BEFORE taking action to make sure that that action is in your best interest?
And better still, what if you could do this with a "scientific" method, rather than just with guess-work?
Understanding how people are likely to react to your choices is important in many areas of business.
For example, imagine that you're competing in a market with a small number of other companies. If you can anticipate their moves, then you can either remove some of their options, or beat them when they make their moves.
Game Theory gives you the tools you need to think about this.
What is Game Theory?
Game theory is a reasoned attempt to predict behavior. It applies in situations where an individual's success in making choices depends on the choices of others. Simple models include a group of players, a definition of the actions that those players can choose, and the "payoffs" (how much each player will win or lose) for each combination of actions.
John von Neumann and Oskar Morgenstern defined the foundations of game theory in 1944 with their classic book, "Theory of Games and Economic Behavior."
Simultaneous and Sequential Games
Situations described by game theory fall into two main categories:
- Simultaneous move games – Here, players make their moves at the same time. Examples include the scissors-paper-stone game, or situations where competing companies launch new products at the start of a year.
- Sequential move games – Here, players take turns making moves. These include chess, or situations where two competing companies react in turn to one another's pricing changes.
We'll look at simultaneous-move games first.
To work out what action to take, players in simultaneous-moves games need to draw up what's called a payoff table before they start. This quantifies the consequences of the different moves that the players involved could take. Using the simplest example of just two players who take just one move each, and have only two options for that move, there are four possible outcomes:
- Both players make Move A.
- Player 1 makes Move A, Player 2 makes Move B.
- Player 1 makes Move B, Player 2 makes Move A.
- Both players make Move B.
This situation can be applied to an example of two widget manufacturers, who are the only competitors in a niche market. Each currently has 50% market share, and sales of $2million a year.
With advances in component technology, it would now be possible for each of them to develop the next generation of widget, but this will cost $500,000 to bring to market.
If both develop the new widgets, the overall market will grow by 10%, as some existing customers will upgrade.
If only one develops the new widget, that company will increase its market share to 75%, but the overall market will only grow by 5% as some existing customers will stay loyal to the supplier who doesn't offer the new product.
If neither company develops the new widget, sales will remain as they are.
The payoff table for this situation (see below) shows the sales income each player would expect in the first year of each of the four possible outcomes. (Results for Company 1 are shown first, and those for Company 2 are shown second.)
| Company 2 – does nothing | Company 2 – develops new widget | |
|---|---|---|
| Company 1 – does nothing | $2,000,000, $2,000,000 | $1,050,000, $3,150,000 |
| Company 1 – develops new widget | $3,150,000, $1,050,000 | $2,200,000, $2,200,000 |
However, the cost of developing the new widget also needs to be taken into account, so the table below removes this cost from sales figures:
| Company 2 – does nothing | Company 2 – develops new widget | |
|---|---|---|
| Company 1 – does nothing | $2,000,000, $2,000,000 | $1,050,000, $2,650,000 |
| Company 1 – develops new widget | $2,650,000, $1,050,000 | $1,700,000, $1,700,000 |
So what should the two companies do?
Well, it's clear that the best outcome for either company would be for it to develop the new widget, and for its competitor to do nothing. But neither can know what the other will do.
If either company does nothing, it risks a large drop in income of nearly 50% if the other company develops the new product. On the other hand, if it goes ahead, it might do extremely well if the other company does nothing, or experience a relatively smaller drop in income after the cost of development, if the other company goes ahead too.
The wise option is clearly to go ahead, however managers need to be careful to prepare for the possible downsides that could occur if their competitors also develop new products. (In fact, if both competitors are analyzing the situation rationally, it's likely that both will develop the new widget, and both will see a reduction in this year's profits.)
Tip:
When thinking about what your competitor will do, assume that he or she will make the best possible choice for themselves. Don't assume that their decision will be random!
The Prisoner's Dilemma
The "Prisoner's Dilemma" game is a classic example of game theory. Two prisoners are held as joint suspects in a burglary, and each is offered the following deal:
- If neither prisoner confesses to the burglary, each will go to jail for one year.
- If one prisoner confesses and agrees to testify against the other, but the other does not confess, then the confessing prisoner will go free, while the silent prisoner will go to jail for five years.
- If both prisoners confess, then both will serve a prison sentence of three years.
For simultaneous-move games in general, we can create a "payoff table" that shows the different combinations of choices. The entries in the table show how much each player (prisoner) wins or loses in each case.
Our payoff table in this example is below ("-1" means a one-year jail sentence, and so on):
| Prisoner 1 says nothing | Prisoner 1 confesses | |
|---|---|---|
| Prisoner 2 says nothing | -1, -1 | 0, -5 |
| Prisoner 2 confesses | -5, 0 | -3, -3 |
Here's the dilemma: In theory, the prisoners' joint best interest is to both say nothing and accept one year each in jail. The problem is that neither is sure if the other will confess to avoid jail completely. So both prisoners end up confessing and serving three years, instead of just one year.
Sequential Move Games and Game Trees
For a sequential move game in which players take turns to move, one after the other, we create a "game tree" (similar to a decision tree ) instead of a payoff matrix. A game tree starts from a single point, and then branches out into the different moves possible for the first player. Each of these possible moves then branches out again to cover all of the possible responses to that move by the second player, and so on.
Most negotiations are considered sequential-move games, and you can represent them with game trees. For example, imagine that a bakery wants to purchase a new van to make deliveries. They approach a dealer, who offers a van that meets their needs at a price of $18,000.
The bakery makes the first decision. There are three options: accept the offer, reject the offer, or ask for a better price.
In response to a rejection, the dealer can walk away or make a better offer. And in response to a request for a better price, the dealer can lower the price or walk away, and so on.
Figure 1 shows a game tree for this negotiation.
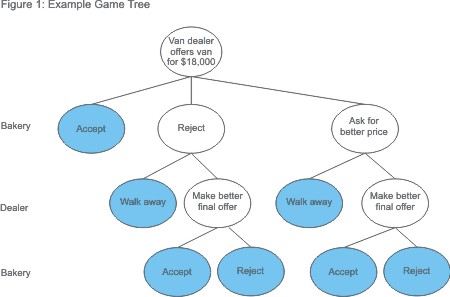
Apart from the simplest cases, game trees can quickly become complex.
Rollback Reasoning
Game trees that describe sequential-move games also let you "look forward and reason backward." This allows you see what your strategy should be now for the best chance of success in the future. This is also known as backward induction.
To determine how the game will unfold, start at the bottom of your tree, and work up, assuming that your opponent makes the best move he or she can each time. As you do, "prune" the branches of the tree that reflect losing choices. What you have left is the likely outcome of the game, assuming that neither player makes a mistake.
Looking at our simple example above, the bakery should ask for a better price, the dealer should give it, and the bakery should accept. Otherwise the dealer loses the sale, and the bakery can't deliver its bread. (Of course, this assumes – among other things – that the dealer needs the sale, and that the bakery doesn't have other, better options.)
When Games Settle into Equilibrium
In many situations (but not always), games settle into a stable situation known in game theory as a "Nash equilibrium" (named after John Nash, another major contributor in this field). In this situation, players know one another's strategies and make the best moves possible in those circumstances. Once they have made these moves, no player has any interest in changing his or her strategy.
A business example is when companies in the same market seek to maximize their profits by each choosing a specific level of output. The best output (and profit) for one company depends on the outputs of the others, so the situation stabilizes into a Nash equilibrium.
Dealing with Real Life
Game theory adapts to additional factors in real-life situations. Even if it uses mathematical formulae to predict outcomes, it also uses common sense to account for the real world. In the prisoner's dilemma, for example, the prisoners might find themselves in the same situation again, as suspects in a second burglary case. However, according to the way they acted the first time, the probabilities of how they'll act this time can change – especially if they now try to avoid errors that they made in the past.
Similarly, in thinking about businesses such as the airline industry, we can go beyond models that are limited to price changes and competitive reactions between existing airline companies. We can start to include additional possibilities – such as other competitors entering the market (low-cost airlines, for instance) or customers switching to other solutions (taking the train, teleconferencing, and so on). And certain choices that airlines make might lead to charges of price-fixing and anti-competitive practices, which can also be modeled using game theory.
You can learn more valuable tips for making the transition from technical expert to manager with our Book Insight on "What Got You Here Won't Get You There" by Marshall Goldsmith.
Key Points
Game theory helps us understand how people act and interact, whether in a business situation or a social environment. Part of game theory deals with basic ideas that you can immediately apply in real life. These include simple tables that show results (payoffs) for different choices, or tree diagrams that follow several steps of an interaction. By looking at the possible outcomes and working backward, you can choose the strategy most likely to give you the best results.
No comments:
Post a Comment